これまで「数」についての記事を書いてきましたが
→算数は面白い 子どもと一緒に学びたい「数」
→子どもと一緒に「もっと」知りたい数の話
もう少しだけ面白い話があるのでお付き合いください
数・算数・数学は本当に広大で不思議です
世の中のミステリーが詰め込まれていると言ってもいいくらいかもしれません。
そんな不可思議なものに親子で一緒に触れられたら・・・とてもステキだとは思いませんか?
一緒にちょっとだけ覗いてみましょう
なに、決して難しくはないのですから・・・

べき乗(指数)と対数
対数とは複雑な掛け算を単純な足し算に変換する方法のことです。
数式で表すと
1,000=10^3(10の3乗)
⇒log10(1,000)=3
とするものです。

難しいことはおいておいて、
この対数を発明したとされるのがスコットランドの数学者ジョン・ネイピアです(その後同僚ヘンリー・ブリッグスが改良)。
彼らは対数表というものを作ったのですが、
簡単に言うとべき乗を足せるようにしたのです。
例えば
100×1000×10000 という計算。
普通に掛け算しても難しい問題ではありませんが、
log10(100)=2
log10(1,000)=3
log10(10,000)=4
なので、2+3+4=9
この9が常用対数で(答えの)10億を表したものです。
インドの伝説で、ヒンドゥー教の僧侶ラフール・セッサの話があります。
ラフール・セッサはチェスのようなゲーム(チャトランガ?)を考え出し、王様に非常に喜ばれました。
望む褒美を聞かれたラフール・セッサは、
「麦をチェスの最初のマス目に1粒ください。2マス目には2粒。その次には4粒と2倍ずつの麦をください。」
と答えました。
王様はそのわずかな要求に大笑いしました。
・・・が、マス目は64マスあります。
最初の1マス目が1粒なので、計算式に表すと
2^63(2の63乗)になります。
これを計算すると、なんと合計
18,446,744,073,709,551,614粒(+1粒)になるのです。

べき乗って恐ろしいですよね(笑)
また、地震にもこの計算が使われています。
地震の大きさを表すリヒタースケール(マグニチュード)は対数で表されており、
マグニチュード1と
マグニチュード9の大きさの違いは
8倍とか9倍大きい、という意味ではなく、
10^8(10の8乗)倍
つまり1億倍の強さなのです。
算数は小さいうちからどうぞ→ワンダーボックス
自然対数e(ネイピア数)
eはすごく説明しづらいものだそうです。
このe(小文字)は、最初、銀行などの利子の複利計算で使われました。
※複利・・・利子にも利子がついていく計算方法
その数式が以下なのですが、
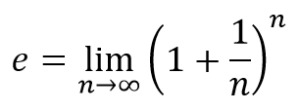
計算はおいておいて、このnに入れる数字をどんどん大きくしていくと、
e=2.7182818284590452353602・・・・・
という無理数になります(どんなにnを大きくしてもこれ以上にならない)
このeという無理数は、自然界でも多く使われていることが解っています。
例えば
・放射性物質の減少
・バクテリアの成長
・貝の渦巻きの長さに対する幅
・冷めてゆくお湯の温度変化
・・・などがあります。
あ、銀行の利息計算でも使われてますね(笑)
自然界でものが増えていく様子をグラフにすると、最初はほぼ水平から始まり、徐々に勾配がきつくなり、ほぼ垂直になって無限大に近づきます。
eは自然界のこの現象をグラフ上で簡単な直線に変えることが出来る数なのです。
今までの記事でも書いてきましたが、
数学というものは本当に自然界において様々な場面で出会いますね。
ちなみに、Google(グーグル)は数学者たちが作った会社だそうです。
2004年、グーグルは株式の売買を開始しましたが、その最初の提示額は
2,718,281,828ドルだったそうです。
↑e億ドルってことですね・・・
また、グーグルと言う社名自体も数学用語の「グーゴルプレックス」から来ているそうです。

超越数
超越数とは、
代数方程式の解にならない数の事を言います。
なんのこっちゃですよね
大丈夫、私もそうです(笑)
これはつまり、
x=2x÷4+5
といった式の場合、x=5ですから、
5と言う数字は超越数ではないのです。
このように代数(xやyなど)方程式の解になり得ない数のこと・・・というのがざっくりとした説明です。
(まぁつまり方程式の答えには絶対ならない数、ということだと思ってください。)
この超越数、有名な所では、
Π(パイ=円周率)
(自然対数)e
リウヴィル数
チャンパーノウン定数
などがあります。
名前もついていない物も含めると、超越数は超越数では無い物(代数方程式の解になれるもの)よりも遥かに多くあるそうです。
始めて発見された超越数は上記にある
リウヴィル数ですが、
自然対数eが超越数か否かを証明する時、フランスの数学者シャルル・エルミートは、
eが代数的数(代数方程式の解になり得る)なら、全ての整数は0と1の間に入る事を示しました。
当然、そんなわけはないのでeは超越数である事が分かったという事です。

メルセンヌ素数
メルセンヌ素数は
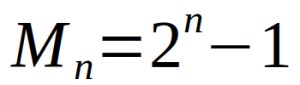
という式が元になっています。
メルセンヌ「素数」というだけあって、
この数式のnには素数を入れます。
例えば、n=2の時、
2×2-1=3
n=3の時
2×2×2-1=7
n=5の時(4は素数ではない)
2×2×2×2×2-1=31
n=7の時
2×2×2×2×2×2×2-1=127
と、答えも素数になっているのです。
こりゃ凄い、面白い!と当時の数学者たちも思ったのですが、
7の次の素数である11の場合、答えが2047になるのですが、
実は因数があることが解りました。(23と89)
素数でない場合はメルセンヌ数と呼ばれます。
ということで、全ての素数がこの式に当てはなるわけではないと解ったわけですが、数学者たちはこの式でどのくらい素数を見つけられるか、に着目していきました。
しかし、作業は難航します。
なぜなら、計算した数字が本当に素数かどうかを判断するのが極めて困難だったからです。

n=13の時、解は8191ですが、これを素数だと証明できたのが1456年のこと
n=17と19は1588年にカタルディによって証明されましたが、
n=31が証明されたのは1772年。レオンハルト・オイラーが素数である事を証明し、
さらにそこから100年ほど経ってからエドゥアール・リュカが
n=127の時の解(2,147,483,647)が素数である事を証明しました。
これまで(2019年末)発見されたメルセンヌ素数は49個あります。
そしてこのメルセンヌ素数は、完全数と不思議な関係がります。
※完全数については前回の記事をどうぞ
→ 子どもと一緒に「もっと」知りたい数の話
完全数のもっとも小さいものは6、その次が28、496、8128とあるのですが、
6=1+2+3
28=1+2+4+7+14
496=1+2+4+8+16+31+62+124+248
8128=1+2+4+8+16+32+64+127+254+508+1016+2032+4064
上の完全数の因数の赤くなっている部分がメルセンヌ素数なのです。
完全数は今のところ49個見つかっており(メルセンヌ素数と同数)、その全てでメルセンヌ素数と関わっているのです。
ちなみに、完全数は無限にあると言われています。
なぜ無限にあるか解るかと言うと、
素数が無限にある事が分かっており、素数の集合に含まれるメルセンヌ素数もまた無限にあり、それが含まれる完全数も無限にある、ということです。
ナンダカスゴイハナシデスネ・・・・
現在見つかっているメルセンヌ素数の中で最大のものは
2^74207281(2の74,207,281乗)-1
で、
22,338,618桁あるそうです。

以上で「数」の不思議な話は終わりにしたいと思います。
ちょっと難しい所も(自分は)ありましたが、
けっこう面白いものですよね
そして数学者の頭の良さには乾杯です
これからも、数の謎を解いて、色々と教えてほしいものですね
あ、なるべく分かり易くお願いしまーす!