以前の記事で「数」についての記事を書きましたが、
算数は面白い 子どもと一緒に学びたい「数」
思ったより好評なので第2回を書いてみようと思います。
「数」は本当に不思議がいっぱい詰まっていますし、秘密がたくさん隠されています。
ともすればその辺のゲームなんかより遥かに面白いものです。
(いや、ゲームも面白いですよ)
今回も「数」にまつわる面白い話を集めてみましたので、お子さんに説明するつもりでみていただければ幸いです
(数学の話が出来る親は頭が良いと思われます!)
完全数
完全数とは、その数の因数(1も含む)の和の合計がその数自身と同じになる数字の事です
※因数・・・その数を割る事の出来る数(約数)のこと
一番小さい完全数は6で、
6の因数は、1、2、3です。
そして
6=1+2+3
これが成立するのが完全数というものです。
他には
28=1+2+4+7+14 496=1+2+4+8+16+31+62+124+248
などがあります。
完全数はメルセンヌ素数という素数の集合に関係があるのですがそれはまた別の機会に・・・
ちなみに数学には「超完全数」と呼ばれるものもあります。
しかし、上記の完全数とは少し別物で、あまり関係はないようです。
また、完全数とは違いますが、友愛数と呼ばれるものもあります。
友愛数とは、 「異なる2つの自然数の組で、その数自身を除いた約数の和が、お互いの数になる組み合わせ」のことです。
例えば220と284という組み合わせです
220の約数の和⇒1+2+4+5+10+11+20+22+44+55+110+220=284
284の約数の和⇒1+2+4+71+142=220
他にも
(1184・1210)、(2620・2924)、 (63020・76084)
などがあります。
友愛数も発見するのは難しかったのですが、オイラーという数学者が発見の法則を見つけ出し、それとコンピュータを組み合わせた現在は、なんと10億組以上の友愛数が確認されているそうです・・・・
フィボナッチ数列
まずはクイズを出してみます。
フィボナッチ数列とは、
ある規則によって出来ている数列のことですが、どうのような規則があるのか、下記の数列を見て考えてみてください
1、1、2、3、5、8、13、21、34、55、89、144、・・・・
この数列は無限に続いていくのですが、どういう規則で並んでいるかおわかりでしょうか?
答えは下記
↓
この数列(フィボナッチ数列)は、
となりの数字を足した答えが次の数字になっているのです。
1+1=2、1+2=3、2+3=5、3+5=8、5+8=13・・・
といった具合です。
この数列を考えたのは13世紀にヨーロッパにアラビア数字を紹介したピサのレオナルドという数学者です。フィボナッチ、というのは彼のあだ名で「ボナッチの息子」という意味です。レオナルド(フィボナッチ)の父親は地元で有名な商人だったそうです。
さて、このフィボナッチ数列、前回の記事の中で書いた黄金比との不思議な関わりがあります。
前回の記事↓
算数は面白い 子供と一緒に学びたい「数」の話
黄金比とは
という比率の事です(クレジットカードがこの黄金比率で作られています)。 正確に言うと (1+√5)÷2=1.16180339887498948482……という無理数なのですが
次にフィボナッチ数列の、ある数とそのひとつ前の数の比率をみてみましょう
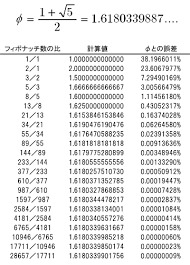
図をご覧いただければお分かりかと思います。
フィボナッチ数列が進めば進むほど、増えれば増えるほど、
ある数とそのひとつ前の数の比率が黄金比に近づいていくのです。
なぜこのような事が起こるのかは解っていませんが、数字の不思議さは感じていただけたのではないでしょうか?
ちょっと休憩
ギリシャの数学者アルキメデスは、その著書「砂の計算書」の中で、
全宇宙に砂粒がどのくらいあるのか、を計算しています
(なんの為でしょう????(笑))
結果、アルキメデスは宇宙には
10^63(10の63乗)粒あると結論付けています。
確認は無理です(笑)
この書物は砂粒の数よりも、初歩的な指数法則の証明がされているのが一番のポイントだったようです。
複素数
複素数と言う名前を聞いたことのある方はけっこう数学が得意な方かも知れませんね
複素数とは何かを説明する前に、虚数の説明が必要になります。
(難しくはないのでご安心ください)
虚数とは数では出来ていない数字の事です
・・・・なんのこっちゃ解りませんよね(笑)
虚数とは1などの数字ではなく、iという代数で出来ています。
詳しく書きますと
i=√-1(ルートマイナス1) です。
つまり、2乗するとマイナス1になるものです。そしてそれを虚数と言います。
掛け算は、
プラス(+)とプラス(+)をかけ合わせればプラス(+)に
(-)×(-)=(+)になりますよね
そして(+)×(-)なら(-)になります。
つまり、2乗した時(全く同じ数字を掛け合わせたとき)には、
マイナスの答えになる数字は存在しないのです。
その存在しないはずのものを作り出したのが「虚数」です。
i×i=-1
さらに「複素数」とは、
実数部分(1など)と虚数部分(i)で出来ている数字の事です。
例)3+4i など
妙に思えるこの「i」は、数学上では驚異的に有用なことが証明されているのです。
なぜ虚数が発明されたかというと、16世紀、多くの数学者がべき乗して3や4になる数を使った複雑な計算を解こうとしていました。
これらの計算には平方根を使うので数学者たちは√-1を使わなければ答えが出ないことに気づいたのです。
そして、1545年、イタリアの変人数学者ジェロラモ・カルダーノが著書「偉大なる術」で虚数を紹介したのです。
ただカルダーノは多くの盗作疑惑があり、本当にカルダーノが発見したものかどうかは怪しいそうです。
(ちなみにカルダーノは後に収監されています。彼は占星術を激しく信じており、自らの死ぬ日を占い、見事に当てたそうです。自殺ですが)
その後、巨匠フリードリヒ・ガウスが実数と虚数の組み合わせを「複素数」と名付け(作ったとされるのはカルダーノの同僚ラファエル・ボンベリ)、数学の幅はどんどん大きくなっていきます。
複素数は、数直線上ではなく、ある種の平面、複素数面を埋めます。実数と虚数はそれぞれ座標のように働くのです。
下の図をご覧ください
↓

この図はフラクタル図形と言われるもので、同じ模様が何度も繰り返されていることが解ると思います。
実はこの図形は複素数を用いて作られており、
自然界にもこの構造をしているものがたくさんあるのです。
野菜のロマネスコなんかがそうですね

また複素数は、
自然音のような乱れた音波を、それぞれ分かり易い単純な曲線に分けることに使われていたり、
波の回転したり上下したりする物の複雑な動きを説明する事にも役立っています。
このように、
虚数および複素数は存在しない数字であるのに、
現実世界は虚数・複素数に満ちているのです
数学って、すごい!と感じちゃいますよね
と、いうわけで今回はここまでにします。
他にも書きたいことはあるのですが、それはまた別の話という事で・・・
数学って難しいと思うのですが、その分、世界の謎を解く、って感じがして面白いですよね
ではまた(^_-)-☆